Goodhart’s Law and the Pitfalls of Targeting Load Port Utilisation on Photo Tools

It has been described as the law that rules the modern world, and its effects can be observed in every organisation. I’m referring to Goodhart’s law, named after British economist Charles Goodhart, who wrote the maxim: “Any observed statistical regularity will tend to collapse once pressure is placed upon it for control purposes.”

A common flavour of this effect is described in the following cartoon, based on a possibly apocryphal story of how central planning failed in a nail factory in the Soviet Union.

We have seen (less dramatic) examples of this effect at work in semiconductor wafer fabs. For instance, teams of operators may be measured on the number of lot moves that occur during their shift. In general, more moves per shift correlates with more wafers delivered on time to customers. However, this relationship breaks down if operators ‘game the system’ by loading batch tools with small batches at the end of the shift, thus wringing out a few extra moves in their shift, but hobbling the next shift.

Memorable though such examples are, they give the impression that Goodhart’s Law relies on people being uninterested in the ultimate goal that their organisation is pursuing. However, apathy is not usually the driving factor in Goodhart’s law; whenever lack of information, limited computational power or even an inability to concisely express our true preferences leads us to substitute a proxy metric for our true goal, the law is bound to rear its head. Former Intel CEO Andy Grove described the effect of such surrogate indicators as like “riding a bicycle: you will probably steer where you are looking”; and if where you’re looking isn’t perfectly correlated with the road ahead, you can expect a wobbly ride!

The intricacies of tools with multiple load ports

For a more subtle example of where using an imperfect measure as a target can lead to suboptimalities when scheduling a wafer fab, we were inspired by a post on the excellent Factory Physics and Automation blog looking at the relationship between load port utilisation and cycle time. In our experience, we have seen load port utilisation of a tool used as a target when designing both operator workflows and dispatching rules.

First, some quick definitions. Many tools in a fab have multiple ‘load ports’ where lots can be inserted into the tool, but then a limited chamber capacity so that, for instance, only one wafer can be processed in the chamber at the same time.

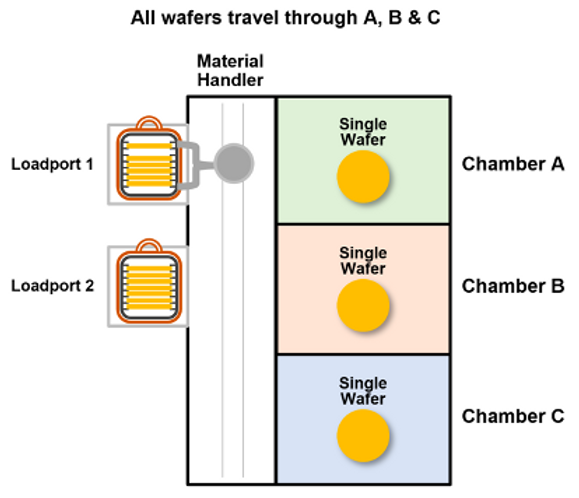
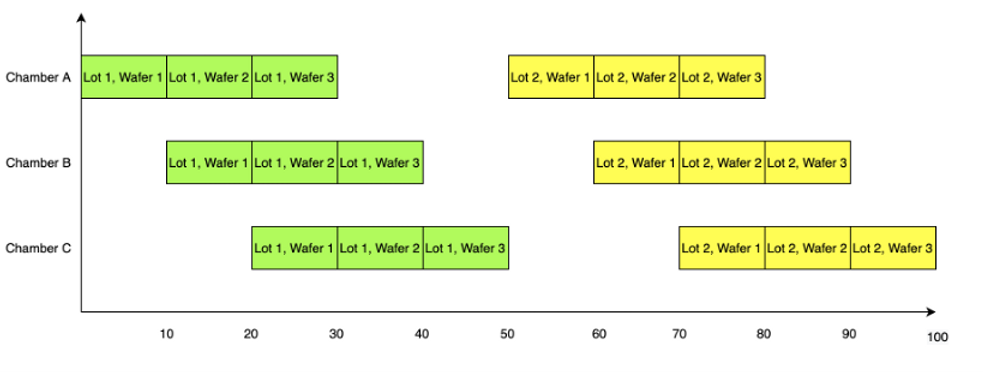
Consider the machine in Fig. 1 with three chambers and two load ports. Lots can be loaded in either load port, but then each wafer in the lot has to move through Chambers A, B and C one at a time. This means wafers may have to queue inside the tool, if the next chamber they need is still processing.  Lots must be unloaded at the same load port in which they were inserted. Suppose it takes each chamber 10 minutes to process a wafer, and we want to process two lots each consisting of three wafers. If we were only allowed to use a single load port, we would have to wait for the first lot to move through all three chambers and exit at the same load port before we can start processing the second lot. Fig.2 shows that for a simple model (that ignores transfer time between chambers), the second lot will have to wait 50 minutes before it can start processing.

If however, an operator loads both batches into the two load ports at the same time (Fig. 3), the machine will pick up the first wafer of the second lot as soon as the first lot has finished processing in chamber A. Thus the second lot will only need to wait 30 minutes.

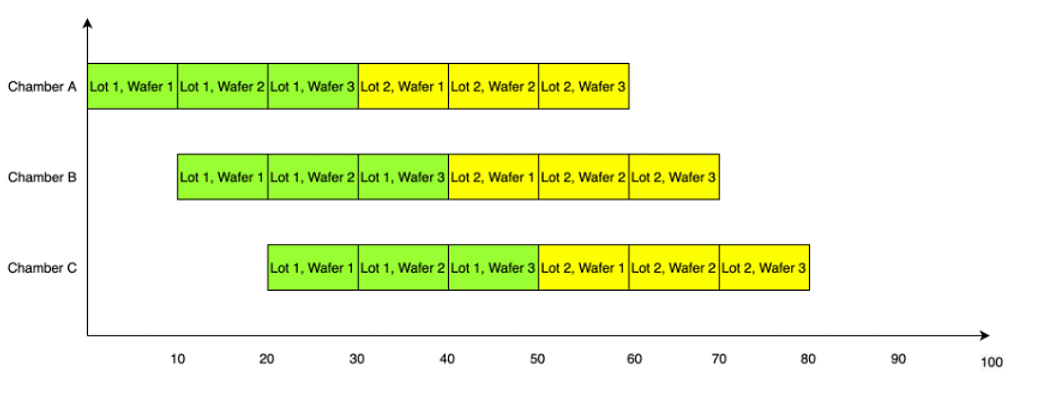
Therefore, for a given level of WIP at a tool, we can expect higher load port utilisation to be correlated with reduced waiting and therefore improved cycle time.

Indeed, in cases where a wafer cannot be unloaded from a tool until all the wafers in the same lot are also ready to be unloaded (a common workflow), it can actually make sense to split lots before a chamber tool. For instance, if we have a lot of 6 wafers before the tool (see Fig. 1) – loading all the wafers as a single lot in a load port – it will take 80 minutes for all 6 wafers to move through the three chambers until we can unload the lot. If however, we split the original lot into two lots of three and load them into both load ports (as in Fig. 3), then the first lot can be unloaded after just 50 minutes, and potentially continue to its next step earlier.

How directly targeting load port utilisation can harm cycle time

As predicted by Goodhart’s Law, the correlation between load port utilisation and fab cycle time breaks down once we try to optimize directly for load port utilisation. This breakdown is particularly stark on photolithography tools, where process steps rely on a critical secondary resource: reticles. Reticles (also called photomasks) act like stencils in the expose step of a photolithography process, patterning the wafer with the desired features.  In most photo tools, reticles must be loaded onto the tool in containers, called pods, before the lots that require them can be loaded onto the machine. Therefore, if a lot is inserted into a load port early, the wafers could just be waiting inside the machine. Moreover, this also requires loading a reticle into the machine when it could have a more productive use elsewhere.

For a simple example, consider a toolset consisting of two of the tools from Fig. 1 (we can imagine chambers A, B and C are performing coat, expose and develop operations respectively).

Suppose we have just loaded a 3 wafer lot onto tool 1. The other load port of tool 1 remains free. Meanwhile on tool 2, both load ports are utilised, but there are only two wafers yet to be processed in Chamber A.

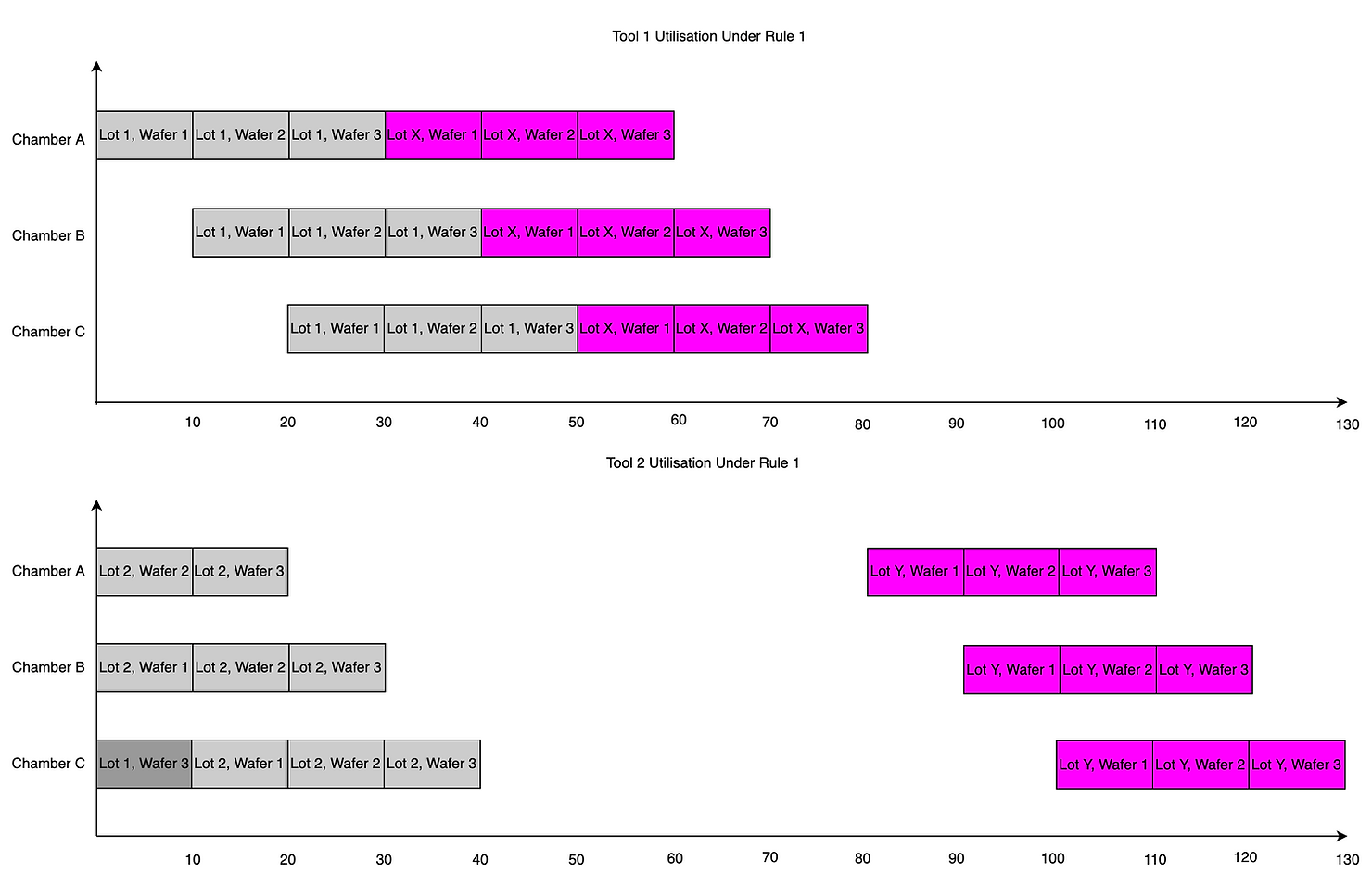
A lot (lot X) that requires a special reticle (of which only one exists) arrives. Due to a lot-level restriction, lot X can only run on tool 1. This sort of restriction is particularly common in photolithography where running consecutive photo layers through the same tool (even if there are multiple tools qualified for the operation) can reduce product variability caused by idiosyncratic aspects of the lensing to a particular tool (this is sometimes known as a ‘lot-to lens’ dedication).The operators on this toolset abide by the following rule for dispatching lots:

Rule 1: If a load port and the required reticle are available, load the reticle and the lot onto the tool.

Since tool 1 has a load port available, the operator immediately loads the reticle onto the machine, and puts lot X into the load port.

Ten minutes later, lot Y arrives at the toolset, also requiring the same reticle, and with a lot-level restriction forcing it to run on tool 2. Since the reticle is already loaded on tool 1, lot Y cannot be dispatched until lot X has finished processing and the reticle has been moved from tool 1 to tool 2. Assume, for the purpose of simplicity, the reticle moves instantaneously, both lots will have finished processing in 130 minutes time (see Fig. 4).

Imagine, however, the operators adopted the following workflow:

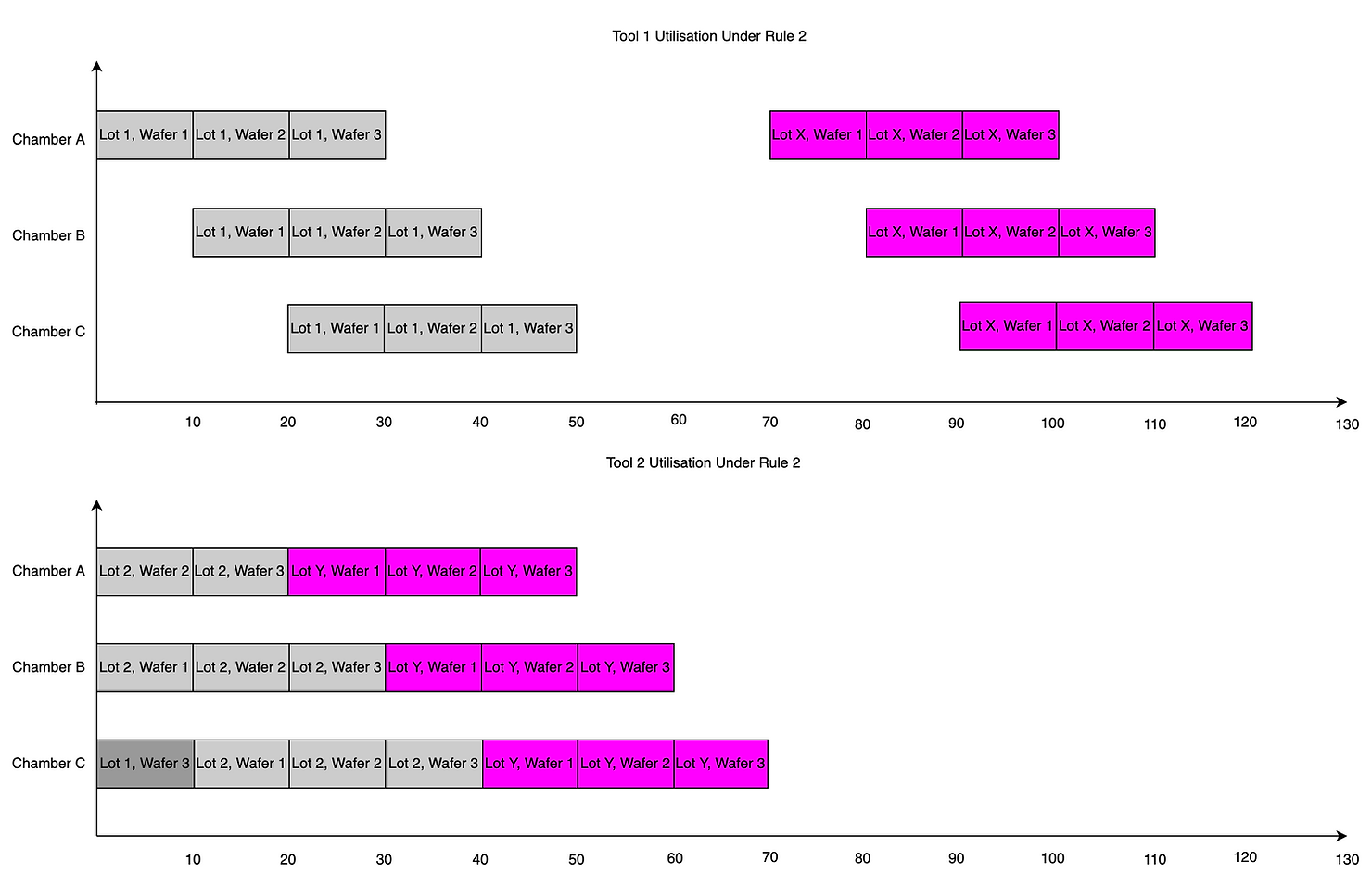
Rule 2:  If a load port and the required reticle are available and the tool can begin processing immediately (i.e. Chamber A is free), load the reticle and the lot onto the tool

In this case, lot X will not be immediately loaded onto tool 1, since Chamber A is initially occupied. After only 20 minutes though, lot Y can be loaded onto tool 2, to finish processing 50 minutes later, at which the reticle can be moved and lot X can start on tool 1. Thus, after just 120 minutes (as opposed to the 130 minutes under Rule 1), both lot X and lot Y will have finished processing. Therefore, we can see that by adopting rule 2, the cycle time, and hence the throughput of the toolset can be improved.

In our experience of wafer fabs, we often see workflows akin to Rule 1, wherein operators fill the load ports of photo tools as soon as they are free, thus forfeiting the opportunity to use reticles earlier on different tools. Adopting a workflow like Rule  2, however, is more difficult since it requires operators to have foreknowledge of when the tool will be ready to process a new lot, and reacting promptly to load the tool at precisely this time.  In practice, particularly when operator availability is limited, you will risk increasing wait time because you leave the tool under utilised if you fail to load a lot as soon as a machine becomes available.

Using advanced optimization to handle Goodhart's Law

Flexciton’s scheduler can help to alleviate this problem by employing advanced optimization technology. It can predict when lots will arrive at the photo toolset and which reticles they will require, and then jointly schedule the reticles and lots on the toolset to obtain an optimized schedule. The knowledge of future arrivals crucially allows us to identify cases where loading a reticle onto a machine now is suboptimal, since a lot will soon arrive at another tool that can make use of the reticle sooner or that simply has a higher priority. Thus, following a Flexciton schedule, operators can dispatch to load ports when they become available, with minimal risk of harming cycle time due to locking in reticles prematurely.

However, we still are not immune to the curse of Goodhart’s Law. The cycle time of an optimized schedule is itself only a proxy for what we actually care about: producing more high quality wafers at a low cost per wafer. Over-optimizing for cycle time may lead to a solution with so many loads and unloads that the labour cost of running fab becomes prohibitive. Or, as described in one of our previous blog posts, the solution may require moving reticles so frequently between tools that we increase the chance of a costly breakage.

To solve this, we apply a technique suggested by Andy Grove himself: we use pairing indicators. Combining indicators, where one has an effect counter to the other, avoids the trap of optimizing one at the expense of another. This is why we typically pair cycle time with the number of batches (to account for limited operator availability) or the number of reticle moves (to keep the risk of reticle damage low), thus mitigating the perils of Goodhart’s Law.

‍